day11-数据结构与算法

Go学习路线 字节跳动青训营
发布日期:   2022-11-05
更新日期:   2024-12-28
文章字数:   4k
阅读时长:   19 分
阅读次数:  

这是我参与「第三届青训营 -后端场」笔记创作活动的的第11篇笔记。PC端阅读效果更佳，点击文末：阅读原文即可。

「数据结构与算法」 第三届字节跳动青训营 - 后端专场

课程背景

  • 这节课是介绍生产环境使用的算法和数据结构，然后重点从排序算法这个在课本上耳熟能详的算法分类开始，一步步打造出一个在工程实践领域性能一流的排序算法，介绍目前工业界最新的实践成果。

课程大纲

01 为什么要学习数据结构与算法

举个例子

  • 规则：某个时间段内，直播间礼物数TOP10房间获得奖励，需要在每个房间展示排行榜

  • 解决方案

    • 礼物数量存储在Redis-zset中，使用skiplist使得元素整体有序
    • 使用Redis集群，避免单机压力过大，使用主从算法、分片算法
    • 保证集群原信息的稳定，使用一致性算法
    • 后端使用缓存算法(LRU)降低Redis压力，展示房间排行榜
数据结构和算法几乎存在于程序开发中的所有地方

什么是最快的排序算法?

具体看特殊场景。

  • Python —-timsort

  • C + + —-introsort

  • Rust—- pdqsort

Go的排序算法有没有提升空间?

Go(< := 1.18) — introsort

课程讲师是给go官方提供了重新实现go排序算法

重新实现了Go的排序算法，在某些常见场景中比之前算法快~ 10倍，成为Go 1.19的默认排序算法

02 经典排序算法

插入排序

将元素不断插入已经排序好的array中

  • 起始只有一个元素5，其本身是一个有序序列
  • 后续元素插入有序序列中，即不断交换，直到找到第一个比其小的元素

时间复杂度：

最好 平均 最坏
$O(n)$ $O(n^2)$ $O(n^2)$

Quick Sort 快速排序

分治思想，不断分割序列直到序列整体有序

  • 选定一个pivot (轴点)
  • 使用pivot分割序列，分成元素比pivot大和元素比pivot小两个序列

时间复杂度：

最好 平均 最坏
$O(n*logn)$ $O(n*logn)$ $O(n^2)$

Heap Sort 堆排序

利用堆的性质形成的排序算法

  • 构造一个大顶堆
  • 将根节点(最大元素)交换到最后一个位置，调整整个堆，如此反复

时间复杂度：

最好 平均 最坏
$O(n*logn)$ $O(n*logn)$ $O(n*logn)$

结论

  • 插入排序平均和最坏情况时间复杂度都是$O(n^2)$，性能不好
  • 快速排序整体性能处于中间层次
  • 堆排序性能稳定，“众生平等”

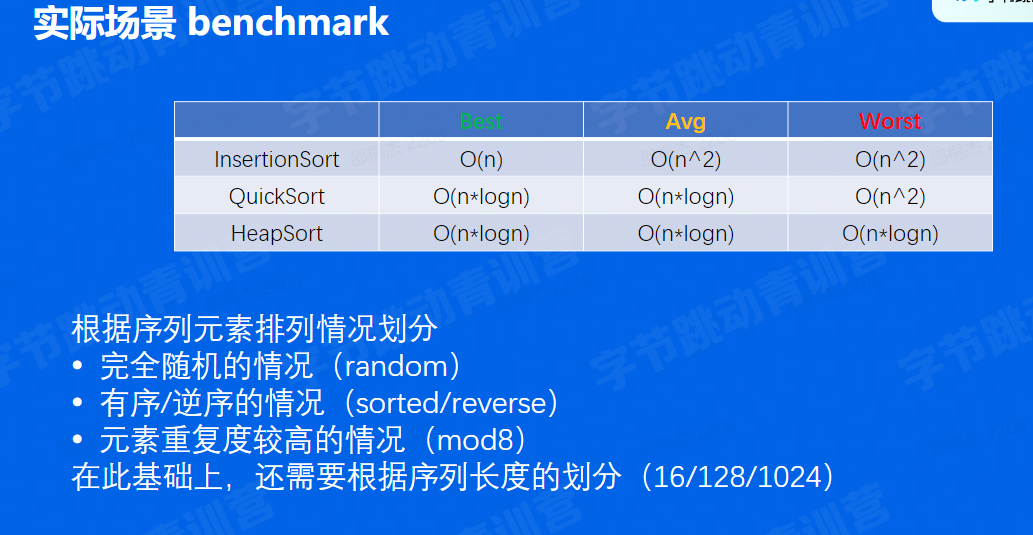
实际场景benchmark

根据序列元素排列情况划分

  • 完全随机的情况(random)
  • 有序/逆序的情况(sorted/reverse)
  • 元素重复度较高的情况(mod8)

在此基础上，还需要根据序列长度的划分(16/128/1024)

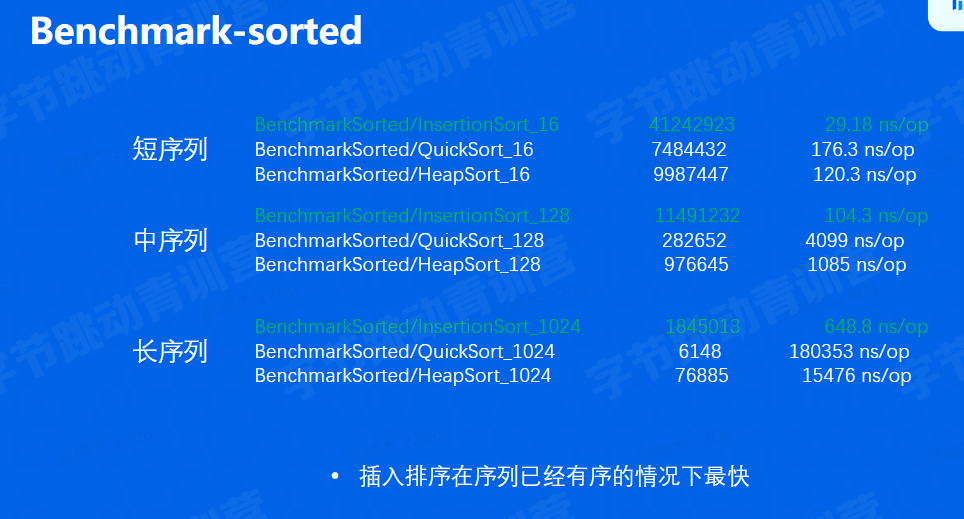03 从零开始打造pdqsort

pdqsort -简介

pdqsort (pattern- defeating-quicksort)

是一种不稳定的混合排序算法，它的不同版本被应用在C++，BOOST、Rust 以及Go 1.19中。它对常见的序列类型做了特殊的优化，使得在不同条件下都拥有不错的性能

pdqsort - version1

结合三种排序方法的优点

对于短序列(小于一定长度)，我们使用插入排序。其他情况，使用快速排序来保证整体性能。

当快速排序表现不佳时，使用堆排序来保证最坏情况下时间复杂度仍然为 $O(n*logn)$

Q&A

  1. 短序列的具体长度是多少呢?

    • 12 ~ 32，在不同语言和场景中会有不同，在泛型版本根据测试选定24

  2. 如何得知快速排序表现不佳，以及何时切换到堆排序?

    • 当最终pivot的位置离序列两端很接近时(距离小于length/8)判定其表现不佳，当这种情况的次数达到limit (即bits.Len(length)) 时，切换到堆排序。

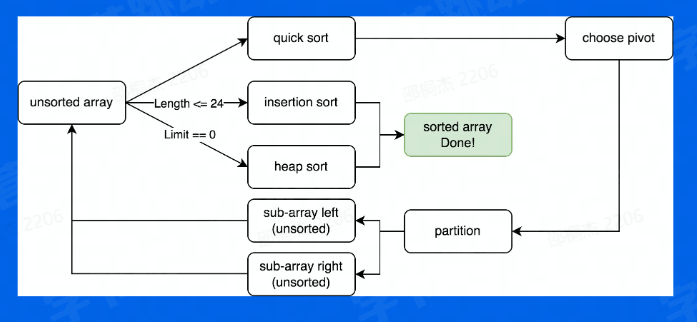
  • 对于短序列(<=24) 我们使用插入排序。
  • 其他情况，使用快速排序(选择首个元素作为pivot)来保证整体性能。
  • 当快速排序表现不佳时(limit==0) ，使用堆排序来保证最坏情况下时间复杂度仍然为O(n*logn)。

如何让pdqsort速度更快?

  • 尽量使得QuickSort的pivot为序列的中位数 -> 改进choose pivot
  • Partition速度更快->改进partition，但是此优化在Go表现不好，略

pdqsort - version2

思考关于pivot的选择

  • 使用首个元素作为pivot(最简单的方案)，实现简单，但是往往效果不好，例如在sorted情况下性能很差
  • 遍历数组，寻找真正的中位数遍历比对代价很高，性能不好

根据序列长度的不同，来决定选择策略

  • 优化 - Pivot的选择
    • 短序列(<=8)，选择固定元素
    • 中序列(<=50)，采样三个元素
    • 长序列(>50)，采样九个元素

Pivot的采样方式使得我们有探知序列当前状态的能力！

  • 采样的元素都是逆序排列—-序列可能已经逆序—-翻转整个序列
  • 采样的元素都是顺序排列—-序列可能已经有序—-使用插入排序

注：插入排序实际使用partiallnsertionSort，即有限制次数的插入排序。

Version1升级到version2优化总结

  • 升级pivot选择策略(近似中位数)
  • 发现序列可能逆序，则翻转序列->应对reverse场景
  • 发现序列可能有序，使用有限插入排序->应对sorted场景

还有什么场景我们没有优化?

  • 短序列情况

    • 使用插入排序(v1)

  • 极端情况

    • 使用堆排序保证算法的可行性(v1)

  • 完全随机的情况(random)

    • 更好的pivot选择策略(v2)

  • 有序/逆序的情况(sorted/reverse)

    • 根据序列状态 翻转或者插入排序(v2)

  • 元素重复度较高的情况(mod8) -> ?

pdqsort - final version

如何优化重复元素很多的情况?

  • 采样pivot的时候检测重复度？不是很好，因为采样数量有限，不一定能采样到相同元素

解决方案:

  • 如果两次partition生成的pivot相同，即partition进行了无效分割，此时认为pivot的值为重复元素
    (相比上一种方法有更高的采样率)

优化-重复元素较多的情况(partitionEqual)

  • 当检测到此时的pivot和上次相同时(发 生在leftSubArray)
    使用partitionEqual将重复元素排列在一起，减少重复元素对于pivot选
    择的干扰

优化-当pivot选择策略表现不佳时，随机交换元素

  • 避免一些极端情况使得QuickSort总是表现不佳，以及一些黑客攻击情况

高性能的排序算法是如何设计的?

  • 根据不同情况选择不同策略，取长补短

生产环境中使用的的排序算法和课本上的排序算法有什么区别?

  • 理论算法注重理论性能，例如时间、空间复杂度等。生产环境中的算法需要面对不同的实践场景，更加注重实践性能

Go语言(<= 1.18)的排序算法是快速排序么?

  • 实际一直是混合排序算法，主体是快速排序。Go <= 1.18时的算法也是基于快速排序，和pdqsort的区别在于fallback时机、pivot 选择策略、是否有针对不同pattern优化等

最后

欣赏一波大佬贡献的代码：

https://github.com/golang/go/blob/master/src/sort/zsortinterface.go

// Code generated by gen_sort_variants.go; DO NOT EDIT.

// Copyright 2022 The Go Authors. All rights reserved.
// Use of this source code is governed by a BSD-style
// license that can be found in the LICENSE file.

package sort

// insertionSort sorts data[a:b] using insertion sort.
func insertionSort(data Interface, a, b int) {
	for i := a + 1; i < b; i++ {
		for j := i; j > a && data.Less(j, j-1); j-- {
			data.Swap(j, j-1)
		}
	}
}

// siftDown implements the heap property on data[lo:hi].
// first is an offset into the array where the root of the heap lies.
func siftDown(data Interface, lo, hi, first int) {
	root := lo
	for {
		child := 2*root + 1
		if child >= hi {
			break
		}
		if child+1 < hi && data.Less(first+child, first+child+1) {
			child++
		}
		if !data.Less(first+root, first+child) {
			return
		}
		data.Swap(first+root, first+child)
		root = child
	}
}

func heapSort(data Interface, a, b int) {
	first := a
	lo := 0
	hi := b - a

	// Build heap with greatest element at top.
	for i := (hi - 1) / 2; i >= 0; i-- {
		siftDown(data, i, hi, first)
	}

	// Pop elements, largest first, into end of data.
	for i := hi - 1; i >= 0; i-- {
		data.Swap(first, first+i)
		siftDown(data, lo, i, first)
	}
}

// pdqsort sorts data[a:b].
// The algorithm based on pattern-defeating quicksort(pdqsort), but without the optimizations from BlockQuicksort.
// pdqsort paper: https://arxiv.org/pdf/2106.05123.pdf
// C++ implementation: https://github.com/orlp/pdqsort
// Rust implementation: https://docs.rs/pdqsort/latest/pdqsort/
// limit is the number of allowed bad (very unbalanced) pivots before falling back to heapsort.
func pdqsort(data Interface, a, b, limit int) {
	const maxInsertion = 12

	var (
		wasBalanced    = true // whether the last partitioning was reasonably balanced
		wasPartitioned = true // whether the slice was already partitioned
	)

	for {
		length := b - a

		if length <= maxInsertion {
			insertionSort(data, a, b)
			return
		}

		// Fall back to heapsort if too many bad choices were made.
		if limit == 0 {
			heapSort(data, a, b)
			return
		}

		// If the last partitioning was imbalanced, we need to breaking patterns.
		if !wasBalanced {
			breakPatterns(data, a, b)
			limit--
		}

		pivot, hint := choosePivot(data, a, b)
		if hint == decreasingHint {
			reverseRange(data, a, b)
			// The chosen pivot was pivot-a elements after the start of the array.
			// After reversing it is pivot-a elements before the end of the array.
			// The idea came from Rust's implementation.
			pivot = (b - 1) - (pivot - a)
			hint = increasingHint
		}

		// The slice is likely already sorted.
		if wasBalanced && wasPartitioned && hint == increasingHint {
			if partialInsertionSort(data, a, b) {
				return
			}
		}

		// Probably the slice contains many duplicate elements, partition the slice into
		// elements equal to and elements greater than the pivot.
		if a > 0 && !data.Less(a-1, pivot) {
			mid := partitionEqual(data, a, b, pivot)
			a = mid
			continue
		}

		mid, alreadyPartitioned := partition(data, a, b, pivot)
		wasPartitioned = alreadyPartitioned

		leftLen, rightLen := mid-a, b-mid
		balanceThreshold := length / 8
		if leftLen < rightLen {
			wasBalanced = leftLen >= balanceThreshold
			pdqsort(data, a, mid, limit)
			a = mid + 1
		} else {
			wasBalanced = rightLen >= balanceThreshold
			pdqsort(data, mid+1, b, limit)
			b = mid
		}
	}
}

// partition does one quicksort partition.
// Let p = data[pivot]
// Moves elements in data[a:b] around, so that data[i]<p and data[j]>=p for i<newpivot and j>newpivot.
// On return, data[newpivot] = p
func partition(data Interface, a, b, pivot int) (newpivot int, alreadyPartitioned bool) {
	data.Swap(a, pivot)
	i, j := a+1, b-1 // i and j are inclusive of the elements remaining to be partitioned

	for i <= j && data.Less(i, a) {
		i++
	}
	for i <= j && !data.Less(j, a) {
		j--
	}
	if i > j {
		data.Swap(j, a)
		return j, true
	}
	data.Swap(i, j)
	i++
	j--

	for {
		for i <= j && data.Less(i, a) {
			i++
		}
		for i <= j && !data.Less(j, a) {
			j--
		}
		if i > j {
			break
		}
		data.Swap(i, j)
		i++
		j--
	}
	data.Swap(j, a)
	return j, false
}

// partitionEqual partitions data[a:b] into elements equal to data[pivot] followed by elements greater than data[pivot].
// It assumed that data[a:b] does not contain elements smaller than the data[pivot].
func partitionEqual(data Interface, a, b, pivot int) (newpivot int) {
	data.Swap(a, pivot)
	i, j := a+1, b-1 // i and j are inclusive of the elements remaining to be partitioned

	for {
		for i <= j && !data.Less(a, i) {
			i++
		}
		for i <= j && data.Less(a, j) {
			j--
		}
		if i > j {
			break
		}
		data.Swap(i, j)
		i++
		j--
	}
	return i
}

// partialInsertionSort partially sorts a slice, returns true if the slice is sorted at the end.
func partialInsertionSort(data Interface, a, b int) bool {
	const (
		maxSteps         = 5  // maximum number of adjacent out-of-order pairs that will get shifted
		shortestShifting = 50 // don't shift any elements on short arrays
	)
	i := a + 1
	for j := 0; j < maxSteps; j++ {
		for i < b && !data.Less(i, i-1) {
			i++
		}

		if i == b {
			return true
		}

		if b-a < shortestShifting {
			return false
		}

		data.Swap(i, i-1)

		// Shift the smaller one to the left.
		if i-a >= 2 {
			for j := i - 1; j >= 1; j-- {
				if !data.Less(j, j-1) {
					break
				}
				data.Swap(j, j-1)
			}
		}
		// Shift the greater one to the right.
		if b-i >= 2 {
			for j := i + 1; j < b; j++ {
				if !data.Less(j, j-1) {
					break
				}
				data.Swap(j, j-1)
			}
		}
	}
	return false
}

// breakPatterns scatters some elements around in an attempt to break some patterns
// that might cause imbalanced partitions in quicksort.
func breakPatterns(data Interface, a, b int) {
	length := b - a
	if length >= 8 {
		random := xorshift(length)
		modulus := nextPowerOfTwo(length)

		for idx := a + (length/4)*2 - 1; idx <= a+(length/4)*2+1; idx++ {
			other := int(uint(random.Next()) & (modulus - 1))
			if other >= length {
				other -= length
			}
			data.Swap(idx, a+other)
		}
	}
}

// choosePivot chooses a pivot in data[a:b].
//
// [0,8): chooses a static pivot.
// [8,shortestNinther): uses the simple median-of-three method.
// [shortestNinther,∞): uses the Tukey ninther method.
func choosePivot(data Interface, a, b int) (pivot int, hint sortedHint) {
	const (
		shortestNinther = 50
		maxSwaps        = 4 * 3
	)

	l := b - a

	var (
		swaps int
		i     = a + l/4*1
		j     = a + l/4*2
		k     = a + l/4*3
	)

	if l >= 8 {
		if l >= shortestNinther {
			// Tukey ninther method, the idea came from Rust's implementation.
			i = medianAdjacent(data, i, &swaps)
			j = medianAdjacent(data, j, &swaps)
			k = medianAdjacent(data, k, &swaps)
		}
		// Find the median among i, j, k and stores it into j.
		j = median(data, i, j, k, &swaps)
	}

	switch swaps {
	case 0:
		return j, increasingHint
	case maxSwaps:
		return j, decreasingHint
	default:
		return j, unknownHint
	}
}

// order2 returns x,y where data[x] <= data[y], where x,y=a,b or x,y=b,a.
func order2(data Interface, a, b int, swaps *int) (int, int) {
	if data.Less(b, a) {
		*swaps++
		return b, a
	}
	return a, b
}

// median returns x where data[x] is the median of data[a],data[b],data[c], where x is a, b, or c.
func median(data Interface, a, b, c int, swaps *int) int {
	a, b = order2(data, a, b, swaps)
	b, c = order2(data, b, c, swaps)
	a, b = order2(data, a, b, swaps)
	return b
}

// medianAdjacent finds the median of data[a - 1], data[a], data[a + 1] and stores the index into a.
func medianAdjacent(data Interface, a int, swaps *int) int {
	return median(data, a-1, a, a+1, swaps)
}

func reverseRange(data Interface, a, b int) {
	i := a
	j := b - 1
	for i < j {
		data.Swap(i, j)
		i++
		j--
	}
}

func swapRange(data Interface, a, b, n int) {
	for i := 0; i < n; i++ {
		data.Swap(a+i, b+i)
	}
}

func stable(data Interface, n int) {
	blockSize := 20 // must be > 0
	a, b := 0, blockSize
	for b <= n {
		insertionSort(data, a, b)
		a = b
		b += blockSize
	}
	insertionSort(data, a, n)

	for blockSize < n {
		a, b = 0, 2*blockSize
		for b <= n {
			symMerge(data, a, a+blockSize, b)
			a = b
			b += 2 * blockSize
		}
		if m := a + blockSize; m < n {
			symMerge(data, a, m, n)
		}
		blockSize *= 2
	}
}

// symMerge merges the two sorted subsequences data[a:m] and data[m:b] using
// the SymMerge algorithm from Pok-Son Kim and Arne Kutzner, "Stable Minimum
// Storage Merging by Symmetric Comparisons", in Susanne Albers and Tomasz
// Radzik, editors, Algorithms - ESA 2004, volume 3221 of Lecture Notes in
// Computer Science, pages 714-723. Springer, 2004.
//
// Let M = m-a and N = b-n. Wolog M < N.
// The recursion depth is bound by ceil(log(N+M)).
// The algorithm needs O(M*log(N/M + 1)) calls to data.Less.
// The algorithm needs O((M+N)*log(M)) calls to data.Swap.
//
// The paper gives O((M+N)*log(M)) as the number of assignments assuming a
// rotation algorithm which uses O(M+N+gcd(M+N)) assignments. The argumentation
// in the paper carries through for Swap operations, especially as the block
// swapping rotate uses only O(M+N) Swaps.
//
// symMerge assumes non-degenerate arguments: a < m && m < b.
// Having the caller check this condition eliminates many leaf recursion calls,
// which improves performance.
func symMerge(data Interface, a, m, b int) {
	// Avoid unnecessary recursions of symMerge
	// by direct insertion of data[a] into data[m:b]
	// if data[a:m] only contains one element.
	if m-a == 1 {
		// Use binary search to find the lowest index i
		// such that data[i] >= data[a] for m <= i < b.
		// Exit the search loop with i == b in case no such index exists.
		i := m
		j := b
		for i < j {
			h := int(uint(i+j) >> 1)
			if data.Less(h, a) {
				i = h + 1
			} else {
				j = h
			}
		}
		// Swap values until data[a] reaches the position before i.
		for k := a; k < i-1; k++ {
			data.Swap(k, k+1)
		}
		return
	}

	// Avoid unnecessary recursions of symMerge
	// by direct insertion of data[m] into data[a:m]
	// if data[m:b] only contains one element.
	if b-m == 1 {
		// Use binary search to find the lowest index i
		// such that data[i] > data[m] for a <= i < m.
		// Exit the search loop with i == m in case no such index exists.
		i := a
		j := m
		for i < j {
			h := int(uint(i+j) >> 1)
			if !data.Less(m, h) {
				i = h + 1
			} else {
				j = h
			}
		}
		// Swap values until data[m] reaches the position i.
		for k := m; k > i; k-- {
			data.Swap(k, k-1)
		}
		return
	}

	mid := int(uint(a+b) >> 1)
	n := mid + m
	var start, r int
	if m > mid {
		start = n - b
		r = mid
	} else {
		start = a
		r = m
	}
	p := n - 1

	for start < r {
		c := int(uint(start+r) >> 1)
		if !data.Less(p-c, c) {
			start = c + 1
		} else {
			r = c
		}
	}

	end := n - start
	if start < m && m < end {
		rotate(data, start, m, end)
	}
	if a < start && start < mid {
		symMerge(data, a, start, mid)
	}
	if mid < end && end < b {
		symMerge(data, mid, end, b)
	}
}

// rotate rotates two consecutive blocks u = data[a:m] and v = data[m:b] in data:
// Data of the form 'x u v y' is changed to 'x v u y'.
// rotate performs at most b-a many calls to data.Swap,
// and it assumes non-degenerate arguments: a < m && m < b.
func rotate(data Interface, a, m, b int) {
	i := m - a
	j := b - m

	for i != j {
		if i > j {
			swapRange(data, m-i, m, j)
			i -= j
		} else {
			swapRange(data, m-i, m+j-i, i)
			j -= i
		}
	}
	// i == j
	swapRange(data, m-i, m, i)
}

参考资料：

  1. https://juejin.cn/post/7098278757802180622
  2. https://bytedance.feishu.cn/file/boxcnZoRBfHvkwiwXC5qKft4L7b
文章作者: 千羽
文章链接: https://nateshao.gitlab.io/2022/11/05/day11-shu-ju-jie-gou-yu-suan-fa/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 千羽 !
Go学习路线 字节跳动青训营
赏
评论
  目录